ML & DL/복습

밑바닥부터 시작하는 딥러닝 Chapter 3

후리붜너 2023. 1. 21. 18:37
Repeat is the best medicine for memory.

신경망

 

신경망 구조

신경망은 전 챕터에서 배웠던 퍼셉트론의 구조와 동일하다. 퍼셉트론과 신경망의 차이는 활성화함수인데 이는 뒤에서 더 설명하겠다.

 

신경망의 구조는 위 그림과 같이 입력층, 은닉층, 출력층이 차례대로 나열된 구조이다. 입력층은 입력되는 Feature의 개수만큼의 노드가, 은닉층과 출력층에서는 재표현되는 Feature의 개수만큼의 노드가 존재한다.

 

퍼셉트론과의 차이점

퍼셉트론과 신경망의 차이점은 활성화함수다. 다층퍼셉트론에서 이전층의 출력을 다음층의 입력으로 보낼 때 활성화함수는 계단함수(Step Function)가 사용된다. 하지만 신경망에서는 Step Function이 아닌 sigmoid, softmax같은 연속적인 함수가 활성화함수로 사용된다.

 

Step Function은 불연속적인 함수이기 때문에 Forward Pro(순전파)에서는 문제가 없지만 Back Propogation(역전파)에서는 미분값이 1 또는 0이 되어버려서 연쇄법칙에 의해서 경사도가 0으로 나뉘어야하는 상황이 생긴다. 이 때문에 Step Function은 학습에 사용될 수 없다.

 

활성화 함수

  • 활성화함수를 사용함으로써 비선형적 요소가 적용되고 이는 신경망을 여러 층으로 구성하는 이유가 된다.
  • 계단함수(Step Function)은 불연속 함수로 역전파에 의한 학습이 불가하다 → 신경망에 사용 불가.

 

신경망 구현 (계산)

신경망은 퍼셉트론의 곱과 합 계산방식이 그대로 적용된다. 여기에 활성화함수가 추가되는 것이다.

 

다만 퍼셉트론과는 다르게 신경망의 층마다 한번에 계산이 이루어진다. 이런 이유 때문에 다차원 배열(Matrix)과 내적의 개념이 필요하게 된다.

 

내적

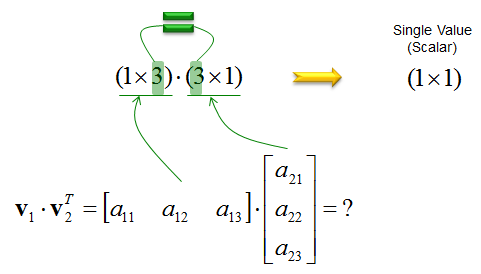
위 그림에서 내적하는 방식을 확인할 수 있다.

  • 첫 번째 다차원 배열의 열 크기와 두 번째 다차원 배열의 행 크기가 같을 때만 내적이 가능하다.
  • 결과로 나오는 배열의 크기는 행 크기가 첫 번째 배열의 행 크기, 두 번째 배열의 열 크기가 된다.

위처럼 신경망의 순전파를 구현할 수 있다.

 

Task에 따른 활성화함수

활성화함수는 위와같이 경우에 따라 다르게 사용된다.

  • 신경망은 분류와 회귀 문제로 구분해서 구현할 수 있다.
  • 출력층을 설계할 때는 어떤 task인지, 그리고 출력의 개수를 잘 설정해야 한다. (분류에서는 분류할 개수로 설정해야함)
  • Softmax에서는 overflow 문제가 있다.

Softmax의 Overflow

Softmax 함수는 아래와 같은 식을 가진다.

Softmax 수식

위와 같은 식을 가지기 때문에 softmax는 overflow가 발생할 수 있는데, 이유는 exponential이라는 지수함수로 큰 값을 만들어 나누기 때문이다.

 

1000이상의 아주 큰 값들이 자연상수의 지수로 오게 되면 표현하기 어려운 아주 큰 값이 되기 때문에 계산 자체가 되지 않을 수도 있다. (numpy 계산에서는 nan으로 나오게 됨.)

 

이 문제를 해결하기 위한 방법은 두 가지가 있는데 

첫 번째는 softmax가 단조 증가 함수임을 사용하는 것이다.

 

Softmax함수는 단조 증가 함수이기 때문에 어떤 수로 이루어진 배열이 있을 때 그 배열을 softmax에 넣기 전과 넣은 후의 크기 순서는 동일하다. (대소 관계가 동일하다.) 이런 특징을 사용해서 실제 실무에서는 다중분류 문제가 존재할 때 추가적인 연산이 필요한 softmax를 사용하지 않고 바로 argmax를 통한 분류를 진행한다.

 

두 번째 방법은 overflow 자체를 막는 방법이다. softmax에는 배열이 입력으로 주어지는데, softmax를 적용하기 전에 그 배열의 값들을 일정한 상수로 모두 뺄셈을 수행하는 것이다. 이렇게 뺄셈을 진행하면 배열 내 수들 크기가 작아져서 overflow가 발생하지 않을 수 있다. 일반적으로는 배열에서 가장 큰 값을 빼는 값으로 설정한다고 한다.

 

배치 처리

우리는 지금까지 신경망의 계산을 하나의 입력을 가정하고 진행해왔다. 사실 이렇게 입력을 하나씩 진행하면 학습하는데 시간이 엄청나게 소요된다. 때문에 신경망 학습에는 배치 처리라는 방법을 사용한다.

 

배치 처리는 단순하게 여러 개의 입력을 일정 개수로 묶어 한번에 forward를 진행시키는 것이다.

예를 들어, 한 장의 이미지를 입력으로 넣는 것이 아니라 4, 8개씩 이미지를 묶어서 한번에 하나의 배열로 신경망에 입력시키는 것이다.

 

배치 처리가 좋은 이유는 두 가지가 있다.

  • 수치 계산 라이브러리 대부분이 큰 배열을 효율적으로 처리할 수 있도록 고도로 최적화되어 있기 때문.
  • 큰 신경망에서는 데이터 전송이 병목으로 작용할 수 있는데, 배치 처리를 함으로써 부하를 줄일 수 있기 때문. (정확히는 I/O를 통해 데이터를 읽는 횟수가 줄어서 빠른 CPU나 GPU로 순수 계산을 수행하는 비율이 높아지기 때문이라고 한다.)

결론적으로 컴퓨터에서는 큰 배열을 한번에 계산하는 것이 작은 배열을 여러 번 계산하는 것보다 빠르다.