ANN (Artificial Neural Network) 인공신경망

인공신경망 (ANN)

인공신경망은 은닉층이 적은 neural network 알고리즘에서 은닉층의 개수가 많아 깊어지는 neural network를 의미한다. 

 

머신러닝에서 배운 Linear Regression(회귀)과 Logistic Regression(분류)는 은닉층이 없는 neural network로 구현이 가능하다.

ANN의 구조

 

NN의 구조 및 구조 해석

NN의 구조는 keras에서 Dense로 불리는 완전연결층을 갖는다. 이전 layer의 노드들과 다음 layer의 노드들이 모두 연결되어 있기에 완전연결이라고 한다. 노드들의 간선에는 W라는 가중치가 존재하여 노드가 갖는 값(feature)에 선형적인 연산이 포함되게 된다. 이때 노드로 표시되지는 않지만 bias라는 편향이 노드가 하나 더 있는 것처럼 작용한다.

 

NN에서 노드의 역할

선형연산이 모두 끝났다면 일반적으로 합연산이 진행되고 마지막으로 activation function이 적용된다.

activation function은 활성화함수로 선형적인 연산만으로 표현할 수 없는 feature들을 설명하기 위해 사용된다. 

다양한 활성화함수(activation function)가 존재하지만 일반적으로 회귀는 linear, 이진분류는 sigmoid, 다중 분류는 softmax가 사용되며 은닉층에서는 relu가 사용된다.

 

활성화함수는 model 내부에서 은닉층이 어떻게 사용되는지, 문제가 어떤 것인지에 따라 바뀔 수 있다.

 

노드의 의미

만약 우리의 모델이 NN이라고 할 때 어떤 은닉층의 노드 수가 증가하고 감소하는 데에 있어서 성능이 변한다면 어떻게 해석해야 할까?

 

전통적인 머신러닝이나 초기의 딥러닝 NN의 경우에는 학자들이 feature engineering을 통해 모델이 데이터를 잘 설명하도록 feature를 추가시켜줬다. 하지만 잘 알다시피 데이터를 잘 설명할 수 있는 feature들을 인간이 모두 설명할 수는 없다. 이에 딥러닝을 활용해 설명력은 떨어지지만 성능을 높일 수 있는 딥러닝이 등장한다.

 

기본적으로 NN layer의 노드는 feature를 의미한다. input으로 input feature가 들어오게 되면 선형적인 연산과 활성화함수(비선형적 연산)로 새로운 feature를 추출하고 이 과정을 여러번 거치면서 추상화하여 우리가 원하는 Y값이 나오도록 예측하는 것이다. 

 

즉, 이런 예를 통해 이해할 수 있겠다. 만약 노드의 개수가 은닉층에서 늘어났을 때 모델의 성능이 증가한다면 그 모델의 그 은닉층은 더 많은 feature를 표현할 수 있던 상태였던 것이고 노드를 줄였을 때 모델의 성능이 좋아졌다면 그 노드가 의미하는 feature는 없는 것이 낫다고(의미없다고) 판단할 수 있을 것이다.

 

은닉층의 의미

은닉층의 의미는 노드의 의미와 유사하지만 약간 다르다.

이전 은닉층의 노드들이 선형적으로 연산된 결과들을 합하여 비선형적인 연산을 통해 새로운 feature들이 도출되는데 이것이 은닉층이다. 

 

즉, 은닉층은 이전 은닉층의 feature로부터 새롭게 표현되는 feature라고 생각할 수 있다.

이를 통해 모델의 feature를 재표현하는 과정이 많이 필요한 경우는 깊게, 아니라면 얕게 만들어야겠다고 생각할 수도 있겠다.

 

만약 은닉층을 추가했는데 모델의 성능이 좋아졌다면 그 모델이 나타내려는 데이터는 이전 모델이 나타내려는 데이터보다 더 고수준(더 추상화된)의 feature로 추출되었을 때 비슷하다고 볼 수 있다.

반대로 은닉층을 줄였을 때 모델의 성능이 좋아졌다면 너무 추상화를 많이해 데이터를 더 복잡하게 표현해려고 했던 것이다.

 

 

 

은닉층과 노드의 수로 ML에서 인간이 직접 feature engineering을 했던 수고를 덜 수 있으며 또한 더 좋은 성능을 가진 모델을 설계할 수도 있다. 이런 과정을 feature representation이라고 한다. (컴퓨터가 feature를 재표현하는 과정)

 

활성화 함수(Activation Function)

Sigmoid

Sigmoid 함수는 아래와 같은 식으로 정의된다.

시그모이드 식

시그모이드는 입력 x에 대해서 exponential의 음수 지수값으로 사용되면서 1을 더하고 역수가 취해져 0부터 1사이의 값이 결과로 나오도록 유도된다. 시그모이드는 일반적으로 이진분류에서 True인지 False인지 판단하도록 0~1사이의 확률값을 도출하기 위해서 사용된다.

sigmoid 그래프

시그모이드는 위와 같은 그래프를 가진다. y값이 0과 1에 가까울수록 기울기가 작은 것을 볼 수 있는데 이는 NN에서 backpropagation 과정에서 gradient Vanishing 문제를 일으키게 된다. 

Softmax

Softmax는 sigmoid와 비슷하게 분류를 위해 확률값을 도출하도록 설계된 함수이다.

수식은 아래와 같다.

softmax 식

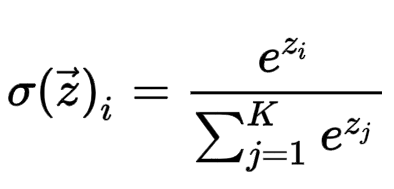
시그모이드와는 다르게 각 값들의 합이 반드시 1이 되며, 가장 높은 값이 다중분류 문제에서 예측값이 되도록 설계되었다.

softmax는 cross entropy와 수학적으로 아주 관련이 많다. 이는 나중에 다룰 예정이다.

 

Relu

relu는 위에서 언급한 gradient vanishing 문제를 개선하기 위해 NN의 은닉층에서 자주 사용된다.

relu의 수식은 아래와 같다.

relu 식

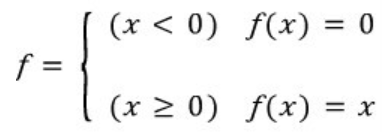
relu는 sigmoid가 활성화함수로 사용되며 은닉층이 깊어질 때 계속해서 1보다 작은 경사도의 곱으로 인해 뒤에서 앞으로 역전파가 진행될수록 점점 경사도가 작아지는 문제를 개선한다. 

 

relu의 그래프는 아래와 같다.

relu 그래프

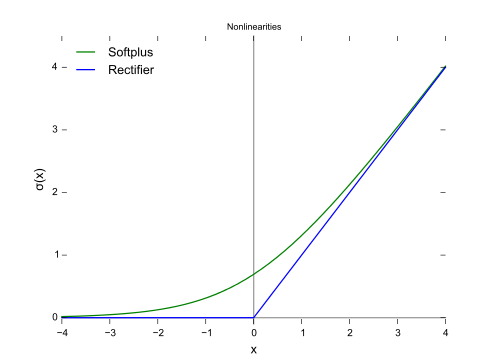
이외에 leaky relu, swish, softplus등 여러가지 활성화함수가 존재하지만 모두 다 다루지는 않겠다.

 

 

추가

추가적으로 교육을 받으면서 배운 부분들이 있다.

Early Stopping

Early Stopping은 모델의 학습중에 어떤 지표값을 기준으로 더 이상 모델의 성능이 좋아지지 않을 때 학습을 중단하여 시간적 비용을 줄이고 최적 값을 찾도록 도와주는 기능이다.

from tensorflow.keras.callbacks import EarlyStopping

es = EarlyStopping(monitor='val_loss',
                   min_delta=0,
                   patience=5,
                   verbose=1,
                   restore_best_weights=True)
                
model.fit(train_x, train_y, validation_split=0.2, callbacks=[es],
          verbose=1, epochs=50)

 

위의 코드처럼 EarlyStopping을 선언하고 model이 학습할 때 callbacks의 옵션에 넣어주기만 하면 된다.

 

Early Stopping의 인자로 monitor는 어떤 것을 보고 stop할 것인지 지표를 정하는 옵션이고,

min_delta는 값이 min_delta만큼 차이가 커지지 않았을 때는 증가했다고 판단하지 않도록 하는 옵션이다.

가장 중요한 patience는 단어 patience(인내심)의 뜻에서 유추할 수 있듯이 값이 증가하지 않는 epoch 횟수가 얼마나 지속될 때 stop할 것인지에 대한 옵션이다. 

 

model이 학습할 때 callbacks라는 인자에 넣어주고 validation_split으로 학습하는 데이터를 validation 분할하여 early stopping이 validation에 대한 loss를 볼 수 있도록 했다.

 

SGD와 BGD

Gradient Descent는 경사하강법이라 불리며 인공신경망에서 backpropagation에 사용되는 알고리즘이다. 경사하강법은 가중치와 bias가 가지는 경사도를 구해 learning rate와 함께 다음 학습전에 update되며 최적값에 도달하도록 사용된다.

일반적인 SGD와 BGD의 개념은 구글링을 통해 어디서나 확인할 수 있으므로 한가지 궁금했던 점만 짚고 넘어가도록 하겠다.

 

SGD는 빠르게 갱신하는 대신 한 데이터를 볼 때마다 갱신하기 때문에 여기저기 튀는 부분이 있다. 하지만 BGD는 모든 데이터를 한번에 보고 갱신하기 때문에 튀지않고 매우 안정적을 최적화한다.

 

우리가 사용하는 실세계 데이터들은 딱 하나의 최적지점이 존재하는 것이 아니기 때문에 최적화를 진행할 때 여러 알고리즘을 통해 모델이 다른 최적지점을 예상하지 못하도록 해야한다.

이것이 바로 local minimum(minima)이다. 

 

SGD는 랜덤한 값이 들어올때 노이즈를 포함하기 때문에 local minimum을 통과할 가능성이 높다. 하지만 learning rate가 적당히 작고 BGD가 적용된 경우에는 노이즈는 없고 최적의 길로 이동하기 때문에 local minimum에 빠질 가능성이 높다.

 

 

Reference

https://medium.com/swlh/how-does-stochastic-gradient-descent-find-the-global-minima-cb1c728dbc18

How Does Stochastic Gradient Descent Find the Global Minima?

https://keras.io/api/callbacks/early_stopping/

Keras documentation: EarlyStopping